約数と倍数の問題です。知識としてはテキストの約数倍数を理解していれば解けた問題です。具体的には「余り」に関する論点の中に、「割り切れる数とは?」というポイントがあるのでそこの理解が鍵になります。
学習を終えている方はぜひ見てみてください。
http://www.tokyo23city.or.jp/saiyo/sikenmondai_r03/siken_pdf/ichirui/kyouyou.pdf
(出典:東京都特別区人事委員会)
全体の戦略としては、「200個-アイウに当てはまるボールの個数」で考えていきましょう。
「アの条件のボールがいくつあるか?」と言うのは、シンプルに「7の倍数が200までにいくつあるか?」ということですから、200÷7=28…4よって28個です。イやウも同様に考えるとそれぞれ40個、と100個となります。
さて、ここで注意したいのはアにもイにも当てはまる数、つまり5と7の公倍数のように上の個数の中には複数回数えられているものが含まれています。
では、公倍数について整理していきましょう。
5と7の最小公倍数35ですから200までの中に200÷35=5…25つまり5個あります。
忘れてはならないのが2,5,7の公倍数でこれは最小公倍数が70であることから200÷70=2…60で2個あります。
ですから、5と7の公倍数5個のうち2個は2の倍数であるため2回数えられています
つまり図で表すと次のようになります。
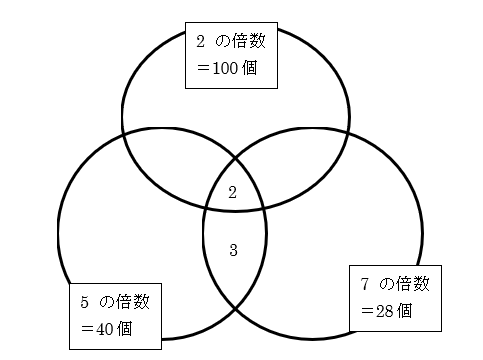
左下と右下の円が重なる部分の個数は5個そして、そのうち、3つの円が重なっている部分の個数は2個だと言えます。
そのようにして重なっている部分を重複して数え無いようにして整理していきます。
2と5の最小公倍数は10なので、200÷10=10個、2と7の最小公倍数は14なので200÷14=14…4の14個になります。
図にまとめると次の通り。
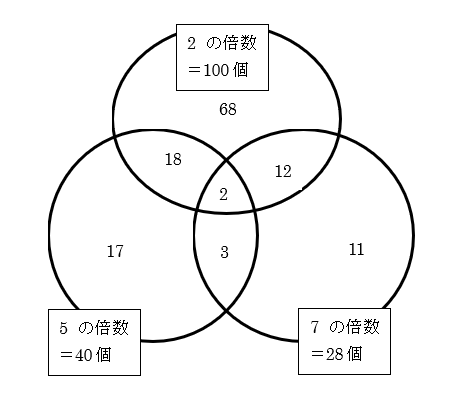
つまり、この三つの円の中には68+18+2+12+17+3+11=131個の整数があると言えます。
本問で問われているのは、200個のボールからこれらを取り出した後残る個数ですから200-131=69
69個が正解です。


