東京都庁１類A採用試験令和３年度（令和３年５月９日第１次試験実施）問12について

（出典：東京都庁ホームページ）

本問は、シンプルな約数・倍数の問題です。

テキストの数的推理の例題をきちんと消化してくださった方は、すぐに手が動いたのではないでしょうか。

まず、200以下の整数のうち、３の倍数がいくつあるかと言えば

200÷３＝66…２

ですから、66個あります。

また、今回、「５でも割り切れないし、６でも割り切れないもの」との指示がありますが、

図としては下記のように整理していきましょう。

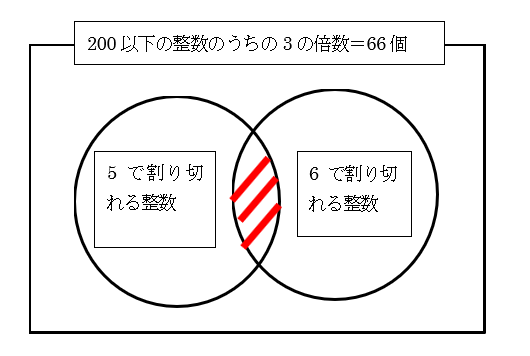
すなわち、66個から内側の二つの円の内部に属する整数の個数を引くことで、今回問われている３の倍数のうち、５でも割り切れないし、６でも割り切れないものの個数を求めるという考え方です（二つの円の外側にある整数の個数を求めます）。

さて、３の倍数のうち、５で割り切れる整数はすなわち、３の倍数でもあり、５の倍数でもある３と５の公倍数です。最小公倍数が15であることから、

200÷15＝13…５

よって、13個

また、３の倍数のうち、６で割り切れる整数は同様に３と６の公倍数と言えますから最小公倍数が６。200以下にいくつあるかと言えば

200÷６＝33…２

つまり33個

さて、ここで忘れてはならないのが二つの円が重なっている赤の斜線部分。ここは２回分数えています。

では、赤の斜線部分に当てはまる整数がいくつあるのかと考えてみると、ここは、３の倍数であって、なおかつ５でも６でも割り切れる整数です。

ということは３,５,６の公倍数だと言えそうです。

最小公倍数が30ですから、200÷30＝６…20

よって6個。

今知りたいのは二つの円の外側の整数の個数でしたね。

66－（13＋33－６）＝26

答は26個です。