基本情報技術者試験に頻出するアルゴリズムについて解説！

アルゴリズムは、基本情報技術者試験の合格のために重要なポイントとなります。しかし、アルゴリズム問題は数学的な要素も多く、苦手という方は多いのではないでしょうか。

アルゴリズムはコンピュータの基本となる大切な要素であり、どうしても避けて通ることはできません。この記事では、基本情報技術者で問われるアルゴリズムの種類やその概要について解説しますので、アルゴリズム問題を苦手にしている方は参考にしてみてください。

アルゴリズムとは

アルゴリズムとは、コンピュータにプログラム処理をさせるときの処理手順を示したものです。コンピュータの世界においては、あらゆる場面で登場する定型的な処理というものが存在します。それが、情報を探す「探索」や情報を並び替える「整列」といった処理です。

コンピュータ上で効率的に探索や整列を行うために、様々な処理手順（＝アルゴリズム）が考え出されました。そして、様々なアルゴリズムの中から、計算コストが少ない優秀なアルゴリズムが採用されるようになりました。

探索アルゴリズム

探索アルゴリズムは、探索を行うためのアルゴリズムのことです。ここでは、基本情報技術者試験で問われる探索アルゴリズムについて解説します。

探索とは

探索とは、ふだん私たちがGoogleなどを利用して行っているように、ある条件に一致する情報を見つけ出す処理を指します。Googleであれば、キーワードに一致するWebページを探し出しますね。

コンピュータの世界においては、より基本的な探索が多数行われています。例えば、コンピュータが画面に画像を表示するときには、その画像データを広大なメモリやHDDから探し出す処理が行われています。また、自動運転では車載カメラから得られた画像データを探索し、信号機や交差点などを自動認識します。

このように、コンピュータの世界において探索は多数利用されており、できるだけ効率的に探索するためのアルゴリズムが必要とされているのです。

線形探索法

線形探索法は、最も基本的な探索アルゴリズムです。線形探索法はまたの名を逐次探索法といい、その言葉通り単純に探索の対象とするデータ群と探索したいデータである探索値を先頭から比較していき、目的のデータが見つかるまで探索を続ける方法です。

【例】
探索値：6

データ群：

4	3	6	3	1
1回目×	2回目×	3回目〇

→3回で探索完了

単純な方法とはいえ、整列されていない乱雑に集められたデータを捜索する際には効率的な探索アルゴリズムとなります。総当たりとなるため、大量のデータを探索するのには向いていません。

線形探索法によってN個のデータ群の探索が完了するまでに必要となる平均比較回数は、(N+1) / 2回となります。これは、目的のデータが見つかるまでの最小回数が1回、最大回数がN回と考えるとわかりやすいです。

例えば、3個のデータ群から目的のものを見つけるためには、1回目・2回目・3回目のいずれかの比較で発見できますね。つまり、平均では(3+1) / 2 = 2回で必要なデータを見つけ出すことができます。

2分探索法

2分探索法は、データがあらかじめ整列されているときに用いる探索方法です。整列しているデータの中央値からスタートし、探索値が中央値より大きければ上位に、小さければ下位に向かって検索を行うことを繰り返します。

2分探索法では、1回検索するごとに探索範囲を半分に絞っていくことができます。N個のデータ群の場合の平均比較回数は、log2Nとなります。

log2Nとは2をNにする指数の値を指すもので、例えばN=8の場合は、2を8にする指数の値は3であるため、log28 = 3となります。つまり、8個のデータ群を2分探索法で探索する場合の平均比較回数は3回となるわけです。

ハッシュ表探索法

ハッシュ表探索法とは、あらかじめデータをハッシュ化した上で、対象のデータのハッシュ値を求めることで確実にデータを見つける方法です。

ハッシュ化とは、データを決められた計算方法（関数）にかけることで値を算出することを指します。また、ハッシュ化により求められた値をハッシュ値といいます。良く用いられるのが除算の余りでハッシュ化する方法で、例えば2021を10で割った余りでハッシュ化すると、1が2021のハッシュ値となります。

ハッシュ化のメリットはデータの大きさを小さくできることで、探索の際の比較をスピーディに行うことができます。また、あらかじめデータ群をハッシュ化しておくことで、探索値のハッシュ値を求めれば即データを探索することができます。

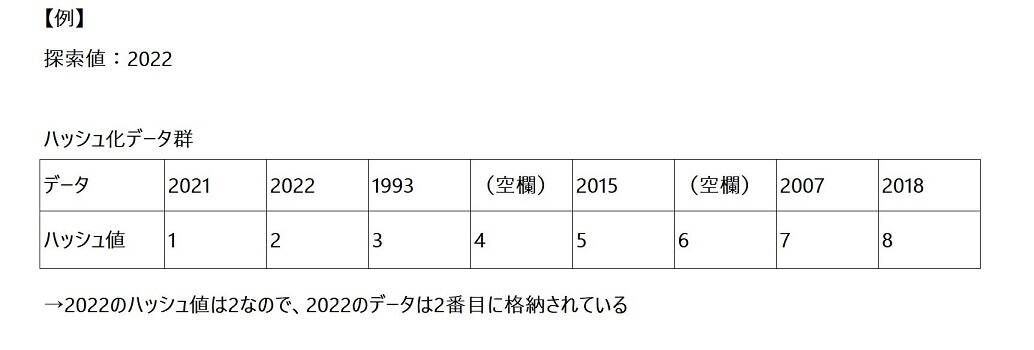
上記のように、ハッシュ値の順に並び替えてデータを格納しておけば、ハッシュ値がそのままデータの格納場所となるため、瞬時にデータを見つけることができます。よって、ハッシュ表探索法の平均比較回数は1回です。

整列アルゴリズム

次に、整列アルゴリズムについて解説します。整列アルゴリズムとは、その名の通り整列を行うためのアルゴリズムのことを指します。

整列（ソート）とは

整列、もしくはソートとは、データを大小関係に応じて並び替えることを指します。大きい順に並べることを降順ソート、小さい順に並び替えることを昇順ソートとい言います。Excel表などを利用するときに、データを日付や個数、金額などで並び替えることがあると思いますが、このような操作がソートの代表例となります。

ソートはその利用範囲の広さから、コンピュータにおいて最も重要な操作と言えるかもしれません。そのため、できるだけ高速にソートができるように、多数の整列アルゴリズムが考え出され、利用されています。

選択ソート

選択ソートは、整列対象とするデータ群の中から最大値もしくは最小値を探し出し、その値を先頭に移動させることを繰り返してソートを行う方法です。

選択ソートは最も単純であり、基本的なソートと言えます。速度は遅いため、現実的に利用されることはありませんが、直感的に理解できるため最初に学ぶべきソートであるといえます。

【例】
昇順に並び替え

データ群：

6

3

4

9

8

★1回目の操作：

6	3	4	9	8
	最小値

→3と6を交換する

3

6

4

9

8

★2回目の操作：

3	6	4	9	8
		最小値

→4と6を交換する

3

4

6

9

8

★3回目の操作：

3	4	6	9	8
		最小値

→操作なし

3

4

6

9

8

★4回目の操作：

3	4	6	9	8
				最小値

→8と9を交換する

3

4

6

8

9

整列完了

選択ソートのデータ比較回数は、最小値または最大値の探索を繰り返すことから、(N-1)+(N-2)+...+1 = N(N-1) / 2 回となります。

バブルソート

バブルソートは隣接するデータの大小関係を比較して、逆順となっていれば並び替えることを繰り返すソート方法です。以下に例を示します。

【例】
昇順に並び替え

データ群：

6

3

4

9

8

★1回目の操作：

6	3	4	9	8
大きい	小さい

→3と6を交換する

3

6

4

9

8

★2回目の操作：

3	6	4	9	8
	大きい	小さい

→4と6を交換する

3

4

6

9

8

★3回目の操作：

3	4	6	9	8
		小さい	大きい

→操作なし

3

4

6

9

8

★4回目の操作：

3	4	6	9	8
			大きい	小さい

→8と9を交換する

3

4

6

8

9

整列完了

バブルソートのデータ比較回数は選択ソートと同様に(N-1)+(N-2)+...+1 = N(N-1) / 2 回となります。

挿入ソート・シェルソート

挿入ソートは、既に整列済みのデータ群に対して適切な位置にデータを挿入していくソート方法です。部分的にソートがされている対象に対してソートを実施する際によく利用される方法です。

【例】
昇順に並び替え

データ群(1～3個目まで整列済み)：

3

4

9

6

8

★1回目の操作：

3	4	9	6	8
			適切な位置に入れる

→4と9の間に6を入れる

3

4

6

9

9

★2回目の操作：

3	4	6	9	8
				適切な位置に入れる

→6と9の間に8を入れる

3

4

6

8

9

整列完了

また、挿入ソートを改良したものにシェルソートと呼ばれるものがあります。詳細は割愛しますが、シェルソートでは一定間隔おきに部分ソートを行い、徐々にその間隔を狭めつつ挿入を行うことで挿入ソートより処理を高速化するものです。

クイックソート

クイックソートはあらかじめ基準値を決めたうえで、その値より大きい群と小さい群に分けることを繰り返すソート方法です。高速でソートを行うことができるため、主流で用いられている方法です。

【例】
昇順に並び替え

データ群：

6

3

4

9

8

★1回目の操作：

6	3	4	9	8
基準値

→基準値より小さいグループと大きいグループに分ける

3

4

6

9

8

★2回目の操作：

3	4	6	9	8
	基準値			基準値

→基準値より小さいグループと大きいグループに分ける

3

4

6

8

9

整列完了

ヒープソート

ヒープソートはまずヒープを作成したうえでヒープの先頭（根）を取り出すことを繰り返すソート方法です。ヒープとは木構造の一種であり、必ず先頭が最大値もしくは最小値となるように構成されています。

ヒープの先頭を取り出した上で、再度ヒープ化を行うと、また先頭が最大値もしくは最小値となるため、その処理を繰り返すことでデータ群をソートすることができます。

ヒープソートは処理速度でクイックソートに劣るため、あまり利用されることはありませんが、部分的に最小値や最大値を取り出す用途で使われることがあります。

再帰アルゴリズム

再帰アルゴリズムとは、その言葉通り再帰を用いたアルゴリズムのことを指します。直感的ではなく実用の場面も少ないため、理解することが難しいアルゴリズムですが、基本情報技術者試験では問われる可能性があるため押さえておくとよいでしょう。

再帰とは

再帰とは、ある処理を入れ子構造のように繰り返し実行することです。ここではカウントアップを行うプログラムを具体例として示します。

ある処理Aでは、与えられた数字を1増やした上で、その数字を画面に表示します。その後、さらに自分自身である処理Aを呼び出して実行するものとします。
処理Aが自分自身である処理Aを実行すると、与えられた数字がさらに1増え、数字が画面に表示されます。そしてさらに処理Aが実行され…ということを繰り返すことになります。

これを図示すると以下のようになります。

このままでは処理Aは無限に繰り返すこととなってしまいますので、一定の回数（例えば値が10にるまで）処理Aが呼び出されたらすべての処理が終了するようにしておきます。

再帰アルゴリズムの例

それでは、このような再帰アルゴリズムはどのような用途があるのでしょうか。再帰アルゴリズムは、主に数学の世界で多く用いられる方法です。有名なものでは、フィボナッチ数列やハノイの塔問題に活用されています。また、一般の利用例としては、掛け算の階乗があげられます。

例えば5!の階乗では、5×4×3×2×1=120という計算を行います。このような処理が、再帰アルゴリズムとぴったりマッチするのです。以下で、再帰アルゴリズムを用いた階乗の例を示します。

アルゴリズムの計算時間

アルゴリズムの効率性は、その計算時間によって計ることができます。アルゴリズムの計算時間はオーダーという指標で表され、O記法によって表現することができます。O記法により各アルゴリズムの性能を表現することで、アルゴリズムの比較を行うことができます。

例えば、探索アルゴリズムであれば線形探索法の平均比較回数は（N+1）/ 2でしたが、これをO記法で表すとO（N）となります。アルゴリズムの計算比較においては、+1や / 2といった大勢に影響を与えない部分は無視します。計算時間の桁数が変わる部分だけ（この例でいえばN）をO記法により表現します。

一方で、2分探索法の平均比較時間はlog2Nであり、O記法で表すとO（log2N）となります。N > log2Nであるため、線形探索法と2分探索法の計算時間を比較すると2分探索法が優れているということになります。

まとめ

この記事では、基本情報技術者試験を受けようとされている方に向けて、アルゴリズムについての解説を行いました。数学が苦手な方にとってはアルゴリズムは難関となるポイントだと思います。

しかしながら、実は基本情報技術者試験で問われるアルゴリズムは基本的なものに限られるため、要点を押さえておけば必要な点数を確保できます。この記事を読んで、分からないところがあれば重点的に学習することをおすすめします。